
Mục lục:
- Tác giả John Day day@howwhatproduce.com.
- Public 2024-01-30 13:37.
- Sửa đổi lần cuối 2025-01-23 15:15.
Giới thiệu
Hướng dẫn này dành cho tất cả mọi người quan tâm đến việc sử dụng Gia tốc kế và Con quay hồi chuyển cũng như các thiết bị IMU kết hợp (Đơn vị đo lường quán tính) trong các dự án điện tử của họ
Chúng tôi sẽ bao gồm:
- Gia tốc kế đo gì?
- Con quay hồi chuyển (hay còn gọi là con quay hồi chuyển) đo gì?
- Cách chuyển đổi các số đọc từ tương tự sang kỹ thuật số (ADC) mà bạn nhận được từ các cảm biến này sang các đơn vị vật lý (chúng sẽ là g đối với gia tốc kế, độ / s đối với con quay hồi chuyển)
- Cách kết hợp các số đọc của máy đo gia tốc và con quay hồi chuyển để có được thông tin chính xác về độ nghiêng của thiết bị của bạn so với mặt đất
Trong suốt bài viết, tôi sẽ cố gắng giữ cho toán học ở mức tối thiểu. Nếu bạn biết Sine / Cosine / Tangent là gì thì bạn sẽ có thể hiểu và sử dụng những ý tưởng này trong dự án của mình cho dù bạn đang sử dụng nền tảng nào: Arduino, Propeller, Basic Stamp, Atmel chip, Microchip PIC, v.v.
Có những người tin rằng bạn cần toán học phức tạp để sử dụng một đơn vị IMU (các bộ lọc FIR hoặc IIR phức tạp như bộ lọc Kalman, bộ lọc Parks-McClellan, v.v.). Bạn có thể nghiên cứu tất cả những thứ đó và đạt được những kết quả tuyệt vời nhưng phức tạp. Cách giải thích của tôi chỉ yêu cầu toán học cơ bản. Tôi là một người rất tin tưởng vào sự đơn giản. Tôi nghĩ rằng một hệ thống đơn giản sẽ dễ dàng điều khiển và giám sát hơn, bên cạnh đó nhiều thiết bị nhúng không có sức mạnh và tài nguyên để thực hiện các thuật toán phức tạp đòi hỏi tính toán ma trận.
Tôi sẽ sử dụng làm ví dụ về đơn vị IMU mới, Gia tốc kế Acc_Gyro + IMU con quay hồi chuyển. Chúng tôi sẽ sử dụng các thông số của thiết bị này trong các ví dụ của chúng tôi bên dưới. Thiết bị này là một thiết bị tốt để bắt đầu vì nó bao gồm 2 thiết bị:
- LIS331AL (bảng dữ liệu) - máy đo gia tốc 2G ba trục - LPR550AL (bảng dữ liệu) - bước và cuộn hai trục, con quay hồi chuyển 500 độ / giây
Chúng cùng nhau đại diện cho Đơn vị đo lường quán tính 5 bậc tự do. Bây giờ đó là một cái tên ưa thích! Tuy nhiên, đằng sau cái tên lạ mắt là một thiết bị kết hợp rất hữu ích mà chúng tôi sẽ đề cập và giải thích chi tiết trong hướng dẫn này.
Bước 1: Gia tốc kế
Để hiểu đơn vị này, chúng ta sẽ bắt đầu với gia tốc kế. Khi nghĩ về gia tốc kế, thường hữu ích khi hình dung một cái hộp có dạng khối lập phương với một quả bóng bên trong nó. Bạn có thể tưởng tượng ra thứ gì đó khác như bánh quy hoặc bánh rán, nhưng tôi sẽ tưởng tượng một quả bóng:
Nếu chúng ta lấy hộp này ở một nơi không có trường hấp dẫn hoặc vì vấn đề đó mà không có trường nào khác có thể ảnh hưởng đến vị trí của quả bóng - quả bóng sẽ chỉ lơ lửng ở giữa hộp. Bạn có thể tưởng tượng chiếc hộp đang ở ngoài không gian rất xa so với bất kỳ thiên thể vũ trụ nào, hoặc nếu khó tìm thấy một nơi như vậy, hãy tưởng tượng ít nhất một tàu vũ trụ quay quanh hành tinh nơi mọi thứ đều ở trạng thái không trọng lượng. Từ hình trên, bạn có thể thấy rằng chúng tôi gán cho mỗi trục một cặp bức tường (chúng tôi đã loại bỏ bức tường Y + để chúng tôi có thể nhìn vào bên trong hộp). Hãy tưởng tượng rằng mỗi bức tường đều nhạy cảm với áp suất. Nếu ta di chuyển đột ngột chiếc hộp sang trái (ta tăng tốc cho nó với gia tốc 1g = 9,8m / s ^ 2) thì quả cầu sẽ đập vào bức tường X-. Sau đó chúng ta đo lực ép mà quả bóng tác dụng lên tường và xuất ra giá trị -1g trên trục X.
Xin lưu ý rằng gia tốc kế sẽ thực sự phát hiện một lực có hướng ngược lại với vectơ gia tốc. Lực này thường được gọi là Lực quán tính hoặc Lực hư cấu. Một điều bạn nên học từ điều này là một gia tốc kế đo gia tốc gián tiếp thông qua một lực tác dụng lên một trong các bức tường của nó (theo mô hình của chúng tôi, nó có thể là một lò xo hoặc một cái gì đó khác trong gia tốc kế ngoài đời thực). Lực này có thể do gia tốc gây ra, nhưng như chúng ta sẽ thấy trong ví dụ tiếp theo, nó không phải lúc nào cũng do gia tốc gây ra.
Nếu chúng ta lấy mô hình của mình và đặt nó trên Trái đất, quả bóng sẽ rơi vào bức tường Z và sẽ tác dụng một lực 1g lên bức tường phía dưới, như thể hiện trong hình dưới đây:
Trong trường hợp này, hộp không di chuyển nhưng chúng tôi vẫn nhận được giá trị -1g trên trục Z. Áp lực mà quả cầu tác dụng lên tường là do lực hút gây ra. Về lý thuyết, nó có thể là một loại lực khác - ví dụ, nếu bạn tưởng tượng rằng quả bóng của chúng ta là kim loại, thì việc đặt một nam châm bên cạnh chiếc hộp có thể di chuyển quả bóng để nó va vào một bức tường khác. Điều này được nói chỉ để chứng minh rằng về bản chất, gia tốc kế đo lực chứ không phải gia tốc. Nó chỉ xảy ra khi gia tốc gây ra một lực quán tính được bắt giữ bởi cơ chế phát hiện lực của gia tốc kế.
Mặc dù mô hình này không chính xác cách cấu tạo cảm biến MEMS nhưng nó thường hữu ích trong việc giải quyết các vấn đề liên quan đến gia tốc kế. Thực tế có những cảm biến tương tự có các quả bóng kim loại bên trong, chúng được gọi là công tắc nghiêng, tuy nhiên chúng nguyên thủy hơn và thường chúng chỉ có thể biết thiết bị có nghiêng trong phạm vi nào đó hay không chứ không phải mức độ nghiêng.
Cho đến nay, chúng tôi đã phân tích đầu ra của gia tốc kế trên một trục duy nhất và đây là tất cả những gì bạn sẽ nhận được với gia tốc kế một trục. Giá trị thực của máy đo gia tốc ba trục đến từ thực tế là chúng có thể phát hiện lực quán tính trên cả ba trục. Hãy quay lại mô hình hộp của chúng ta, và hãy xoay hộp 45 độ sang bên phải. Quả bóng lúc này sẽ chạm vào 2 bức tường: Z- và X- như trong hình dưới đây:
Các giá trị 0,71 không phải là tùy ý, chúng thực sự là một giá trị gần đúng cho SQRT (1/2). Điều này sẽ trở nên rõ ràng hơn khi chúng tôi giới thiệu mô hình tiếp theo của chúng tôi cho gia tốc kế.
Trong mô hình trước, chúng ta đã cố định lực hấp dẫn và quay hình hộp tưởng tượng của chúng ta. Trong 2 ví dụ trước, chúng ta đã phân tích đầu ra ở 2 vị trí hộp khác nhau, trong khi vectơ lực không đổi. Mặc dù điều này hữu ích trong việc hiểu cách gia tốc kế tương tác với các lực bên ngoài, nhưng sẽ thực tế hơn khi thực hiện các phép tính nếu chúng ta cố định hệ tọa độ vào các trục của gia tốc kế và tưởng tượng rằng vectơ lực quay xung quanh chúng ta.
Vui lòng xem mô hình ở trên, tôi đã giữ nguyên màu sắc của các trục để bạn có thể chuyển đổi tinh thần từ mô hình trước đó sang mô hình mới. Chỉ cần tưởng tượng rằng mỗi trục trong mô hình mới vuông góc với các mặt tương ứng của hộp trong mô hình trước đó. Vectơ R là vectơ lực mà gia tốc kế đang đo (nó có thể là lực hấp dẫn hoặc lực quán tính từ các ví dụ trên hoặc kết hợp của cả hai). Rx, Ry, Rz là hình chiếu của vector R trên các trục X, Y, Z. Vui lòng lưu ý mối quan hệ sau:
R ^ 2 = Rx ^ 2 + Ry ^ 2 + Rz ^ 2 (Phương trình 1)
về cơ bản là tương đương với định lý Pitago trong không gian 3D.
Hãy nhớ rằng một chút trước đó tôi đã nói với bạn rằng các giá trị của SQRT (1/2) ~ 0,71 không phải là ngẫu nhiên. Nếu bạn cắm chúng vào công thức ở trên, sau khi nhớ lại rằng lực hấp dẫn của chúng ta là 1 g, chúng ta có thể xác minh rằng:
1 ^ 2 = (-SQRT (1/2)) ^ 2 + 0 ^ 2 + (-SQRT (1/2)) ^ 2
đơn giản bằng cách thay thế R = 1, Rx = -SQRT (1/2), Ry = 0, Rz = -SQRT (1/2) trong phương trình 1
Sau phần mở đầu dài về lý thuyết, chúng ta đang tiến gần hơn đến các máy đo gia tốc trong cuộc sống thực. Các giá trị Rx, Ry, Rz thực sự có liên quan tuyến tính với các giá trị mà gia tốc kế trong đời thực của bạn sẽ xuất ra và bạn có thể sử dụng để thực hiện các phép tính khác nhau.
Trước khi đến đó, chúng ta hãy nói một chút về cách các gia tốc kế sẽ cung cấp thông tin này cho chúng ta. Hầu hết các máy đo gia tốc sẽ thuộc hai loại: kỹ thuật số và tương tự. Gia tốc kế kỹ thuật số sẽ cung cấp cho bạn thông tin bằng cách sử dụng giao thức nối tiếp như I2C, SPI hoặc USART, trong khi gia tốc kế tương tự sẽ xuất ra mức điện áp trong phạm vi được xác định trước mà bạn phải chuyển đổi sang giá trị kỹ thuật số bằng mô-đun ADC (bộ chuyển đổi tương tự sang kỹ thuật số). Tôi sẽ không đi vào chi tiết nhiều về cách thức hoạt động của ADC, một phần vì nó là một chủ đề quá rộng và một phần vì nó khác nhau giữa các nền tảng này. Một số vi điều khiển sẽ có mô-đun ADC tích hợp, một số trong số chúng sẽ cần các thành phần bên ngoài để thực hiện chuyển đổi ADC. Bất kể bạn sử dụng loại mô-đun ADC nào, bạn sẽ nhận được một giá trị trong một phạm vi nhất định. Ví dụ, một mô-đun ADC 10-bit sẽ xuất ra một giá trị trong phạm vi 0..1023, lưu ý rằng 1023 = 2 ^ 10 -1. Mô-đun ADC 12-bit sẽ xuất ra giá trị trong khoảng 0..4095, lưu ý rằng 4095 = 2 ^ 12-1.
Hãy tiếp tục bằng cách xem xét một ví dụ đơn giản, giả sử mô-đun ADC 10bit của chúng tôi đã cung cấp cho chúng tôi các giá trị sau cho ba kênh gia tốc kế (trục):
AdcRx = 586 AdcRy = 630 AdcRz = 561
Mỗi mô-đun ADC sẽ có một điện áp tham chiếu, giả sử trong ví dụ của chúng tôi là 3,3V. Để chuyển đổi giá trị adc 10 bit thành điện áp, chúng tôi sử dụng công thức sau:
VoltsRx = AdcRx * Vref / 1023
Một lưu ý nhanh ở đây: đối với ADC 8 bit, dải chia cuối cùng sẽ là 255 = 2 ^ 8 -1 và đối với ADC 12 bit, dải chia cuối cùng sẽ là 4095 = 2 ^ 12 -1.
Áp dụng công thức này cho cả 3 kênh, chúng tôi nhận được:
VoltsRx = 586 * 3.3V / 1023 = ~ 1.89V (chúng tôi làm tròn tất cả các kết quả đến 2 dấu thập phân) VoltsRy = 630 * 3.3V / 1023 = ~ 2.03V VoltsRz = 561 * 3.3V / 1023 = ~ 1.81V
Mỗi gia tốc kế có một mức điện áp 0 g, bạn có thể tìm thấy nó trong thông số kỹ thuật, đây là điện áp tương ứng với 0g. Để có được giá trị điện áp đã ký, chúng ta cần tính toán sự dịch chuyển từ mức này. Giả sử mức điện áp 0g của chúng ta là VzeroG = 1,65V. Chúng tôi tính toán sự dịch chuyển điện áp từ điện áp zero-g như sau::
DeltaVoltsRx = 1,89V - 1,65V = 0,24V DeltaVoltsRy = 2,03V - 1,65V = 0,38V DeltaVoltsRz = 1,81V - 1,65V = 0,16V
Giờ đây, chúng tôi có số đọc gia tốc kế của mình bằng Volts, nó vẫn chưa tính bằng g (9,8 m / s ^ 2), để thực hiện chuyển đổi cuối cùng, chúng tôi áp dụng độ nhạy của gia tốc kế, thường được biểu thị bằng mV / g. Giả sử Độ nhạy của chúng tôi = 478,5mV / g = 0,4785V / g. Giá trị độ nhạy có thể được tìm thấy trong thông số kỹ thuật của máy đo gia tốc. Để có được giá trị lực cuối cùng được biểu thị bằng g, chúng ta sử dụng công thức sau:
Rx = DeltaVoltsRx / Độ nhạy
Rx = 0,24V / 0,4785V / g = ~ 0,5 gam Ry = 0,38V / 0,4785V / g = ~ 0,79 gam Rz = 0,16V / 0,4785V / g = ~ 0,33 gam
Tất nhiên, chúng ta có thể kết hợp tất cả các bước trong một công thức, nhưng tôi đã xem qua tất cả các bước để làm rõ cách bạn đi từ số đọc ADC sang thành phần vectơ lực được biểu thị bằng g.
Rx = (AdcRx * Vref / 1023 - VzeroG) / Độ nhạy (Eq.2) Ry = (AdcRy * Vref / 1023 - VzeroG) / Độ nhạy Rz = (AdcRz * Vref / 1023 - VzeroG) / Độ nhạy
Bây giờ chúng ta có tất cả 3 thành phần xác định vectơ lực quán tính của chúng ta, nếu thiết bị không chịu các lực khác ngoài lực hấp dẫn, chúng ta có thể coi đây là hướng của vectơ lực hấp dẫn của chúng ta. Nếu bạn muốn tính toán độ nghiêng của thiết bị so với mặt đất, bạn có thể tính toán góc giữa vectơ này và trục Z. Nếu bạn cũng quan tâm đến hướng nghiêng trên mỗi trục, bạn có thể chia kết quả này thành 2 thành phần: độ nghiêng trên trục X và Y có thể được tính như góc giữa vectơ hấp dẫn và trục X / Y. Tính toán các góc này đơn giản hơn bạn có thể nghĩ, bây giờ chúng tôi đã tính toán các giá trị cho Rx, Ry và Rz. Hãy quay lại mô hình gia tốc kế cuối cùng của chúng tôi và thực hiện một số ký hiệu bổ sung:
Các góc mà chúng ta quan tâm là góc giữa các trục X, Y, Z và vectơ lực R. Chúng ta sẽ xác định các góc này là Axr, Ayr, Azr. Bạn có thể nhận thấy từ tam giác vuông tạo bởi R và Rx rằng:
cos (Axr) = Rx / R, và tương tự: cos (Ayr) = Ry / R cos (Azr) = Rz / R
Ta có thể suy ra từ phương trình 1 rằng R = SQRT (Rx ^ 2 + Ry ^ 2 + Rz ^ 2).
Bây giờ chúng ta có thể tìm thấy các góc của chúng ta bằng cách sử dụng hàm arccos () (hàm cos () nghịch đảo):
Axr = arccos (Rx / R) Ayr = arccos (Ry / R) Azr = arccos (Rz / R)
Chúng tôi đã đi một chặng đường dài để giải thích mô hình gia tốc kế, chỉ để đưa ra những công thức này. Tùy thuộc vào ứng dụng của bạn, bạn có thể muốn sử dụng bất kỳ công thức trung gian nào mà chúng tôi đã suy ra. Chúng tôi cũng sẽ sớm giới thiệu mô hình con quay hồi chuyển và chúng ta sẽ xem cách dữ liệu gia tốc kế và con quay hồi chuyển có thể được kết hợp để cung cấp ước tính độ nghiêng chính xác hơn nữa.
Nhưng trước khi chúng ta làm điều đó, hãy thực hiện một số ký hiệu hữu ích hơn:
cosX = cos (Axr) = Rx / R cos = cos (Ayr) = Ry / R cosZ = cos (Azr) = Rz / R
Bộ ba này thường được gọi là Direction Cosine, và về cơ bản nó đại diện cho vectơ đơn vị (vectơ có độ dài 1) có cùng hướng với vectơ R của chúng ta. Bạn có thể dễ dàng xác minh rằng:
SQRT (cosX ^ 2 + cosy ^ 2 + cosZ ^ 2) = 1
Đây là một tính chất tốt vì nó giúp chúng ta không phải theo dõi mô đun (độ dài) của vectơ R. Thông thường, nếu chúng ta chỉ quan tâm đến hướng của vectơ quán tính của mình, thì nên chuẩn hóa mô đun của nó để đơn giản hóa các tính toán khác.
Bước 2: Con quay hồi chuyển
Chúng tôi sẽ không giới thiệu bất kỳ mô hình hộp tương đương nào cho con quay hồi chuyển giống như chúng tôi đã làm cho gia tốc kế, thay vào đó chúng tôi sẽ chuyển thẳng đến mô hình gia tốc kế thứ hai và chúng tôi sẽ hiển thị con quay hồi chuyển đo những gì theo mô hình này.
Mỗi kênh con quay hồi chuyển đo lường chuyển động quay quanh một trong các trục. Ví dụ: con quay hồi chuyển 2 trục sẽ đo vòng quay xung quanh (hoặc một số có thể nói "về") trục X và Y. Để thể hiện vòng quay này bằng số, chúng ta hãy thực hiện một số ký hiệu. Trước tiên, hãy xác định:
Rxz - là hình chiếu của vectơ lực quán tính R trên mặt phẳng XZ Ryz - là hình chiếu của vectơ lực quán tính R trên mặt phẳng YZ
Từ tam giác vuông tạo bởi Rxz và Rz, sử dụng định lý Pitago, ta nhận được:
Rxz ^ 2 = Rx ^ 2 + Rz ^ 2, và tương tự: Ryz ^ 2 = Ry ^ 2 + Rz ^ 2
cũng lưu ý rằng:
R ^ 2 = Rxz ^ 2 + Ry ^ 2, điều này có thể được suy ra từ phương trình 1 trở lên hoặc nó có thể được suy ra từ tam giác vuông tạo bởi R và Ryz R ^ 2 = Ryz ^ 2 + Rx ^ 2
Chúng tôi sẽ không sử dụng các công thức này trong bài viết này nhưng rất hữu ích khi lưu ý mối quan hệ giữa tất cả các giá trị trong mô hình của chúng tôi.
Thay vào đó, chúng ta sẽ xác định góc giữa trục Z và các vectơ Rxz, Ryz như sau:
Axz - là góc giữa Rxz (hình chiếu của R trên mặt phẳng XZ) và trục Z Ayz - là góc giữa Ryz (hình chiếu của R trên mặt phẳng YZ) và trục Z
Bây giờ chúng ta đang tiến gần hơn đến những gì con quay hồi chuyển đo lường. Con quay hồi chuyển đo tốc độ thay đổi của các góc được xác định ở trên. Nói cách khác, nó sẽ xuất ra một giá trị có liên quan tuyến tính với tốc độ thay đổi của các góc này. Để giải thích điều này, hãy giả sử rằng chúng ta đã đo góc quay quanh trục Y (đó sẽ là góc Axz) tại thời điểm t0, và chúng ta xác định nó là Axz0, tiếp theo chúng ta đo góc này sau đó t1 và nó là Axz1. Tỷ lệ thay đổi sẽ được tính như sau:
Tốc độ Axz = (Axz1 - Axz0) / (t1 - t0).
Nếu chúng ta biểu thị Axz bằng độ và thời gian tính bằng giây, thì giá trị này sẽ được biểu thị bằng độ / s. Đây là những gì một con quay hồi chuyển đo lường.
Trong thực tế, một con quay hồi chuyển (trừ khi nó là một con quay hồi chuyển kỹ thuật số đặc biệt) sẽ hiếm khi cung cấp cho bạn một giá trị được biểu thị bằng độ / s. Tương tự như đối với gia tốc kế, bạn sẽ nhận được giá trị ADC mà bạn sẽ cần chuyển đổi thành độ / s bằng cách sử dụng công thức tương tự như Eq. 2 mà chúng tôi đã xác định cho gia tốc kế. Hãy giới thiệu công thức chuyển đổi ADC sang độ / s cho con quay hồi chuyển (giả sử chúng tôi đang sử dụng mô-đun ADC 10 bit, đối với ADC 8 bit thay thế 1023 bằng 255, đối với ADC 12 bit thay thế 1023 bằng 4095).
RateAxz = (AdcGyroXZ * Vref / 1023 - VzeroRate) / Độ nhạy Eq.3 RateAyz = (AdcGyroYZ * Vref / 1023 - VzeroRate) / Độ nhạy
AdcGyroXZ, AdcGyroYZ - được lấy từ mô-đun adc của chúng tôi và chúng đại diện cho các kênh đo lường sự quay của phép chiếu của vectơ R trong XZ tương ứng trong các mặt phẳng YZ, tương đương với việc nói rằng phép quay được thực hiện xung quanh các trục Y và X.
Vref - là điện áp tham chiếu ADC mà chúng tôi sẽ sử dụng 3,3V trong ví dụ bên dưới VzeroRate - là điện áp tỷ lệ 0, nói cách khác là điện áp mà con quay hồi chuyển xuất ra khi nó không chịu bất kỳ vòng quay nào, đối với bảng Acc_Gyro thì ví dụ: 1.23V (bạn có thể tìm các giá trị này trong thông số kỹ thuật) Độ nhạy - là độ nhạy của con quay hồi chuyển của bạn, nó được biểu thị bằng mV / (deg / s) thường được viết là mV / deg / s, về cơ bản nó cho bạn biết bao nhiêu mV sẽ đầu ra con quay hồi chuyển tăng, nếu bạn tăng tốc độ quay thêm một độ / s. Độ nhạy của bảng Acc_Gyro ví dụ như 2mV / deg / s hoặc 0,002V / deg / s
Hãy lấy một ví dụ, giả sử mô-đun ADC của chúng tôi trả về các giá trị sau:
AdcGyroXZ = 571 AdcGyroXZ = 323
Sử dụng công thức trên và sử dụng các tham số thông số kỹ thuật của bảng Acc_Gyro, chúng ta sẽ nhận được:
Tốc độAxz = (571 * 3,3V / 1023 - 1,23V) / (0,002V / độ / s) = ~ 306 độ / s Tốc độAyz = (323 * 3,3V / 1023 - 1,23V) / (0,002V / độ / s) = ~ -94 độ / s
Nói cách khác, thiết bị quay quanh trục Y (hoặc chúng ta có thể nói nó quay trong mặt phẳng XZ) với tốc độ 306 độ / s và quanh trục X (hoặc chúng ta có thể nói nó quay trong mặt phẳng YZ) với tốc độ - 94 độ / s. Xin lưu ý rằng dấu âm có nghĩa là thiết bị quay theo hướng ngược lại với chiều dương thông thường. Theo quy ước một chiều quay là chiều dương. Một bảng thông số kỹ thuật con quay hồi chuyển tốt sẽ cho bạn biết hướng nào là dương, nếu không, bạn sẽ phải tìm nó bằng cách thử nghiệm với thiết bị và lưu ý hướng quay nào dẫn đến tăng điện áp trên chân đầu ra. Điều này được thực hiện tốt nhất bằng cách sử dụng máy hiện sóng vì ngay sau khi bạn dừng vòng quay, điện áp sẽ giảm trở lại mức tỷ lệ bằng không. Nếu bạn đang sử dụng đồng hồ vạn năng, bạn phải duy trì tốc độ quay không đổi trong ít nhất vài giây và ghi lại điện áp trong quá trình quay này, sau đó so sánh nó với điện áp tỷ lệ bằng không. Nếu nó lớn hơn điện áp tỷ lệ 0 thì có nghĩa là chiều quay là dương.
Bước 3: Kết hợp Gia tốc kế và Con quay hồi chuyển
Kết hợp tất cả lại với nhau - Kết hợp dữ liệu gia tốc kế và con quay hồi chuyển
Nếu bạn đang đọc bài viết này, bạn có thể đã mua hoặc đang có kế hoạch mua một thiết bị IMU, hoặc có thể bạn đang dự định chế tạo một thiết bị từ các thiết bị gia tốc kế và con quay hồi chuyển riêng biệt.
Bước đầu tiên khi sử dụng thiết bị IMU kết hợp kết hợp gia tốc kế và con quay hồi chuyển là căn chỉnh hệ tọa độ của chúng. Cách dễ nhất để làm điều đó là chọn hệ tọa độ của gia tốc kế làm hệ tọa độ tham chiếu của bạn. Hầu hết các bảng dữ liệu gia tốc kế sẽ hiển thị hướng của các trục X, Y, Z so với hình ảnh của chip hoặc thiết bị vật lý. Ví dụ đây là hướng của các trục X, Y, Z như được hiển thị trong thông số kỹ thuật cho bảng Acc_Gyro:
Các bước tiếp theo là:
Xác định các đầu ra của con quay tương ứng với các giá trị RateAxz, RateAyz đã thảo luận ở trên
Đừng cho rằng nếu con quay hồi chuyển có đầu ra được đánh dấu X hoặc Y, thì nó sẽ tương ứng với bất kỳ trục nào trong hệ tọa độ gia tốc kế, ngay cả khi đầu ra này là một phần của đơn vị IMU. Cách tốt nhất là kiểm tra nó. Giả sử bạn đã cố định vị trí của con quay hồi chuyển so với gia tốc kế. Giả sử rằng đường viền con quay hồi chuyển và gia tốc kế song song với nhau, tức là bạn đang đặt con quay hồi chuyển ở một góc bội số 90deg so với chip gia tốc. Nếu bạn có được một bảng IMU thì rất có thể chúng đã được căn chỉnh theo cách này. Chúng ta sẽ không thảo luận trong bài viết này về các mô hình mà con quay hồi chuyển được đặt ở một góc không đều so với gia tốc kế (giả sử là 45 hoặc 30 độ), mặc dù điều này có thể hữu ích trong một số ứng dụng.
Dưới đây là một chuỗi mẫu để xác định đầu ra của con quay hồi chuyển tương ứng với giá trị RateAxz đã thảo luận ở trên.
- bắt đầu từ việc đặt thiết bị ở vị trí nằm ngang. Cả hai đầu ra X và Y của gia tốc kế sẽ xuất ra điện áp zero-g (ví dụ: đối với bảng Acc_Gyro, đây là 1,65V)
- tiếp theo bắt đầu xoay thiết bị quanh trục Y, một cách nói khác là bạn xoay thiết bị trong mặt phẳng XZ, sao cho đầu ra gia tốc kế X và Z thay đổi và đầu ra Y không đổi. - trong khi quay thiết bị với tốc độ không đổi, lưu ý rằng đầu ra con quay hồi chuyển thay đổi, các đầu ra con quay hồi chuyển khác sẽ không đổi - đầu ra con quay hồi chuyển thay đổi trong quá trình quay quanh trục Y (quay trong mặt phẳng XZ) sẽ cung cấp giá trị đầu vào cho AdcGyroXZ, từ đó chúng tôi tính RateAxz - bước cuối cùng là đảm bảo hướng quay tương ứng với mô hình của chúng tôi, trong một số trường hợp, bạn có thể phải đảo ngược giá trị RateAxz do vị trí vật lý của con quay hồi chuyển so với gia tốc kế - thực hiện lại bài kiểm tra trên, xoay thiết bị xung quanh trục Y, lần này theo dõi đầu ra X của gia tốc kế (AdcRx trong mô hình của chúng tôi). Nếu AdcRx phát triển (90 độ xoay đầu tiên từ vị trí nằm ngang), thì AdcGyroXZ cũng sẽ phát triển. Nếu không, bạn cần đảo ngược RateAxz, bạn có thể đạt được điều này bằng cách giới thiệu hệ số dấu hiệu trong Eq.3, như sau:
RateAxz = InvertAxz * (AdcGyroXZ * Vref / 1023 - VzeroRate) / Độ nhạy, trong đó InvertAxz là 1 hoặc -1
cùng một cây gậy kiểm tra được thực hiện cho RateAyz, bằng cách xoay thiết bị quanh trục X và bạn có thể xác định đầu ra con quay hồi chuyển nào tương ứng với RateAyz và nếu nó cần được đảo ngược. Khi bạn có giá trị cho InvertAyz, bạn nên sử dụng công thức sau để tính RateAyz:
RateAyz = InvertAyz * (AdcGyroYZ * Vref / 1023 - VzeroRate) / Độ nhạy
Nếu bạn thực hiện các bài kiểm tra này trên bảng Acc_Gyro, bạn sẽ nhận được kết quả sau:
- chân đầu ra cho RateAxz là GX4 và InvertAxz = -1. - chân đầu ra cho RateAyz là GY4 và InvertAyz = -1
Từ thời điểm này trở đi, chúng tôi sẽ xem xét rằng bạn đã thiết lập IMU của mình theo cách mà bạn có thể tính toán các giá trị chính xác cho Axr, Ayr, Azr (như được xác định ở Phần 1. Gia tốc kế) và RateAxz, RateAyz (như được định nghĩa trong Phần 2. Con quay hồi chuyển). Tiếp theo, chúng tôi sẽ phân tích mối quan hệ giữa các giá trị này, những giá trị này sẽ hữu ích trong việc ước tính chính xác hơn độ nghiêng của thiết bị so với mặt đất.
Đến đây bạn có thể tự hỏi mình, nếu mô hình gia tốc kế đã cho chúng ta các góc nghiêng của Axr, Ayr, Azr tại sao chúng ta lại muốn bận tâm đến dữ liệu con quay hồi chuyển? Câu trả lời rất đơn giản: dữ liệu gia tốc kế không phải lúc nào cũng đáng tin cậy 100%. Có một số lý do, hãy nhớ rằng gia tốc kế đo lực quán tính, một lực như vậy có thể do lực hấp dẫn gây ra (và lý tưởng là chỉ do lực hấp dẫn), nhưng cũng có thể do gia tốc (chuyển động) của thiết bị gây ra. Kết quả là ngay cả khi gia tốc kế ở trạng thái tương đối ổn định, nó vẫn rất nhạy cảm với rung động và tiếng ồn cơ học nói chung. Đây là lý do chính tại sao hầu hết các hệ thống IMU sử dụng con quay hồi chuyển để xử lý mọi lỗi gia tốc kế. Nhưng điều này được thực hiện như thế nào? Và con quay hồi chuyển có bị nhiễu không?
Con quay hồi chuyển không có tiếng ồn, tuy nhiên vì nó đo chuyển động quay nên nó ít nhạy cảm hơn với các chuyển động cơ học tuyến tính, loại tiếng ồn mà gia tốc kế phải chịu, tuy nhiên con quay hồi chuyển có các loại vấn đề khác như trôi dạt (không trở về giá trị tốc độ bằng không khi ngừng quay). Tuy nhiên, bằng cách lấy dữ liệu trung bình từ gia tốc kế và con quay hồi chuyển, chúng tôi có thể có được ước tính tương đối tốt hơn về độ nghiêng của thiết bị hiện tại so với những gì chúng tôi có được bằng cách sử dụng dữ liệu gia tốc kế.
Trong các bước tiếp theo, tôi sẽ giới thiệu một thuật toán được lấy cảm hứng từ một số ý tưởng được sử dụng trong bộ lọc Kalman, tuy nhiên nó đơn giản hơn và dễ thực hiện hơn trên các thiết bị nhúng. Trước đó, hãy xem trước tiên chúng ta muốn thuật toán của mình tính toán những gì. Vâng, hướng của vectơ lực hấp dẫn R = [Rx, Ry, Rz] mà từ đó chúng ta có thể suy ra các giá trị khác như Axr, Ayr, Azr hoặc cosX, cosZ, sẽ cho chúng ta ý tưởng về độ nghiêng của thiết bị của chúng ta so với mặt phẳng mặt đất, chúng ta sẽ thảo luận về mối quan hệ giữa các giá trị này trong Phần 1. Người ta có thể nói - không phải chúng ta đã có các giá trị Rx, Ry, Rz này từ phương trình.2 trong Phần 1 rồi sao? Vâng, có, nhưng hãy nhớ rằng các giá trị này chỉ được lấy từ dữ liệu gia tốc kế, vì vậy nếu bạn muốn sử dụng chúng trực tiếp trong ứng dụng của mình, bạn có thể nhận được nhiều tiếng ồn hơn mức mà ứng dụng của bạn có thể chịu đựng. Để tránh nhầm lẫn thêm, hãy xác định lại các phép đo gia tốc kế như sau:
Racc - là vectơ lực quán tính được đo bằng gia tốc kế, bao gồm các thành phần sau (hình chiếu trên các trục X, Y, Z):
RxAcc = (AdcRx * Vref / 1023 - VzeroG) / Độ nhạy RyAcc = (AdcRy * Vref / 1023 - VzeroG) / Độ nhạy RzAcc = (AdcRz * Vref / 1023 - VzeroG) / Độ nhạy
Cho đến nay, chúng tôi có một tập hợp các giá trị đo mà chúng tôi có thể thu được hoàn toàn từ các giá trị ADC của gia tốc kế. Chúng tôi sẽ gọi tập dữ liệu này là "vectơ" và chúng tôi sẽ sử dụng ký hiệu sau.
Racc = [RxAcc, RyAcc, RzAcc]
Vì các thành phần này của Racc có thể thu được từ dữ liệu gia tốc kế, chúng ta có thể coi nó là đầu vào cho thuật toán của mình.
Xin lưu ý rằng vì Racc đo lực hấp dẫn nên bạn sẽ đúng nếu giả sử rằng độ dài của vectơ này được xác định như sau là bằng hoặc gần bằng 1g.
| Racc | = SQRT (RxAcc ^ 2 + RyAcc ^ 2 + RzAcc ^ 2), Tuy nhiên, để chắc chắn, bạn nên cập nhật vectơ này như sau:
Racc (chuẩn hóa) = [RxAcc / | Racc |, RyAcc / | Racc |, RzAcc / | Racc |].
Điều này sẽ đảm bảo độ dài của vectơ Racc chuẩn hóa của bạn luôn là 1.
Tiếp theo, chúng tôi sẽ giới thiệu một vectơ mới và chúng tôi sẽ gọi nó là
Phần còn lại = [RxEst, RyEst, RzEst]
Đây sẽ là kết quả đầu ra của thuật toán của chúng tôi, đây là các giá trị được hiệu chỉnh dựa trên dữ liệu con quay hồi chuyển và dựa trên dữ liệu ước tính trong quá khứ.
Đây là những gì thuật toán của chúng tôi sẽ làm: - gia tốc kế cho chúng tôi biết: "Bây giờ bạn đang ở vị trí Racc" - chúng tôi nói "Cảm ơn bạn, nhưng hãy để tôi kiểm tra", - sau đó sửa thông tin này bằng dữ liệu con quay hồi chuyển cũng như với dữ liệu Nghỉ ngơi trong quá khứ và chúng tôi xuất ra một vectơ ước tính mới Rest. - chúng tôi coi Nghỉ ngơi là "đặt cược tốt nhất" của chúng tôi đối với vị trí hiện tại của thiết bị.
Hãy xem làm thế nào chúng ta có thể làm cho nó hoạt động.
Chúng tôi sẽ bắt đầu trình tự của mình bằng cách tin tưởng vào gia tốc kế của chúng tôi và chỉ định:
Phần còn lại (0) = Racc (0)
Nhân tiện, hãy nhớ Rest và Racc là các vectơ, vì vậy phương trình trên chỉ là một cách đơn giản để viết 3 bộ phương trình và tránh lặp lại:
RxEst (0) = RxAcc (0) RyEst (0) = RyAcc (0) RzEst (0) = RzAcc (0)
Tiếp theo, chúng ta sẽ thực hiện các phép đo thông thường trong khoảng thời gian bằng nhau T giây và chúng ta sẽ thu được các phép đo mới mà chúng ta sẽ định nghĩa là Racc (1), Racc (2), Racc (3), v.v. Chúng tôi cũng sẽ đưa ra các ước tính mới vào mỗi khoảng thời gian Nghỉ ngơi (1), Nghỉ ngơi (2), Nghỉ ngơi (3), v.v.
Giả sử chúng ta đang ở bước n. Chúng tôi có hai bộ giá trị đã biết mà chúng tôi muốn sử dụng:
Phần còn lại (n-1) - ước tính trước đây của chúng tôi, với Phần còn lại (0) = Racc (0) Racc (n) - phép đo gia tốc kế hiện tại của chúng tôi
Trước khi chúng ta có thể tính toán Rest (n), hãy giới thiệu một giá trị đo mới mà chúng ta có thể thu được từ con quay hồi chuyển của mình và ước tính trước đó.
Chúng tôi sẽ gọi nó là Rgyro, và nó cũng là một vectơ bao gồm 3 thành phần:
Rgyro = [RxGyro, RyGyro, RzGyro]
Chúng tôi sẽ tính toán vectơ này một thành phần tại một thời điểm. Chúng ta sẽ bắt đầu với RxGyro.
Hãy bắt đầu bằng cách quan sát mối quan hệ sau đây trong mô hình con quay hồi chuyển của chúng ta, từ tam giác vuông tạo bởi Rz và Rxz, chúng ta có thể suy ra rằng:
tan (Axz) = Rx / Rz => Axz = atan2 (Rx, Rz)
Atan2 có thể là một hàm mà bạn chưa bao giờ sử dụng trước đây, nó tương tự như atan, ngoại trừ nó trả về các giá trị trong phạm vi (-PI, PI) trái ngược với (-PI / 2, PI / 2) do atan trả về và nó mất 2 đối số thay vì một. Nó cho phép chúng ta chuyển đổi hai giá trị Rx, Rz thành các góc trong phạm vi đầy đủ 360 độ (-PI sang PI). Bạn có thể đọc thêm về atan2 tại đây.
Vì vậy, khi biết RxEst (n-1) và RzEst (n-1), chúng ta có thể tìm thấy:
Axz (n-1) = atan2 (RxEst (n-1), RzEst (n-1)).
Hãy nhớ rằng con quay hồi chuyển đo tốc độ thay đổi của góc Axz. Vì vậy, chúng ta có thể ước tính góc mới Axz (n) như sau:
Axz (n) = Axz (n-1) + Tốc độAxz (n) * T
Hãy nhớ rằng RateAxz có thể được lấy từ các bài đọc ADC con quay hồi chuyển của chúng tôi. Một công thức chính xác hơn có thể sử dụng tỷ lệ xoay vòng trung bình được tính như sau:
RateAxzAvg = (RateAxz (n) + RateAxz (n-1)) / 2 Axz (n) = Axz (n-1) + RateAxzAvg * T
Theo cách tương tự chúng ta có thể tìm thấy:
Ayz (n) = Ayz (n-1) + RateAyz (n) * T
Ok vậy bây giờ chúng ta có Axz (n) và Ayz (n). Từ đây chúng ta đi đâu để trừ RxGyro / RyGyro? Từ Eq. 1, chúng ta có thể viết độ dài của vectơ Rgyro như sau:
| Rgyro | = SQRT (RxGyro ^ 2 + RyGyro ^ 2 + RzGyro ^ 2)
Cũng bởi vì chúng tôi đã chuẩn hóa vectơ Racc của mình, chúng tôi có thể giả định rằng độ dài của nó là 1 và nó không thay đổi sau khi xoay, vì vậy tương đối an toàn khi viết:
| Rgyro | = 1
Hãy áp dụng một ký hiệu tạm thời ngắn hơn cho các phép tính dưới đây:
x = RxGyro, y = RyGyro, z = RzGyro
Sử dụng các quan hệ trên, chúng ta có thể viết:
x = x / 1 = x / SQRT (x ^ 2 + y ^ 2 + z ^ 2)
Hãy chia tử số và mẫu số của phân số cho SQRT (x ^ 2 + z ^ 2)
x = (x / SQRT (x ^ 2 + z ^ 2)) / SQRT ((x ^ 2 + y ^ 2 + z ^ 2) / (x ^ 2 + z ^ 2))
Lưu ý rằng x / SQRT (x ^ 2 + z ^ 2) = sin (Axz), do đó:
x = sin (Axz) / SQRT (1 + y ^ 2 / (x ^ 2 + z ^ 2))
Bây giờ nhân tử số và mẫu số của phân số bên trong SQRT với z ^ 2
x = sin (Axz) / SQRT (1 + y ^ 2 * z ^ 2 / (z ^ 2 * (x ^ 2 + z ^ 2)))
Lưu ý rằng z / SQRT (x ^ 2 + z ^ 2) = cos (Axz) và y / z = tan (Ayz), vì vậy cuối cùng:
x = sin (Axz) / SQRT (1 + cos (Axz) ^ 2 * tan (Ayz) ^ 2)
Quay trở lại ký hiệu của chúng tôi, chúng tôi nhận được:
RxGyro = sin (Axz (n)) / SQRT (1 + cos (Axz (n)) ^ 2 * tan (Ayz (n)) ^ 2)
giống như cách chúng tôi tìm thấy điều đó
RyGyro = sin (Ayz (n)) / SQRT (1 + cos (Ayz (n)) ^ 2 * tan (Axz (n)) ^ 2)
Bây giờ, cuối cùng chúng ta có thể tìm thấy:
RzGyro = Dấu (RzGyro) * SQRT (1 - RxGyro ^ 2 - RyGyro ^ 2).
Trong đó Dấu (RzGyro) = 1 khi RzGyro> = 0 và Dấu (RzGyro) = -1 khi RzGyro <0.
Một cách đơn giản để ước tính điều này là:
Sign (RzGyro) = Sign (RzEst (n-1))
Trong thực tế, hãy cẩn thận khi RzEst (n-1) gần bằng 0. Trong trường hợp này, bạn có thể bỏ qua hoàn toàn giai đoạn con quay hồi chuyển và gán: Rgyro = Rest (n-1). Rz được sử dụng làm tham chiếu để tính toán các góc Axz và Ayz và khi nó gần bằng 0, các giá trị có thể chảy quá mức và gây ra kết quả xấu. Bạn sẽ ở trong miền của các số dấu phẩy động lớn nơi triển khai hàm tan () / atan () có thể thiếu chính xác.
Vì vậy, hãy tóm tắt lại những gì chúng ta có cho đến nay, chúng ta đang ở bước n của thuật toán và chúng ta đã tính toán các giá trị sau:
Racc - số đọc hiện tại từ gia tốc kế Rgyro của chúng tôi - thu được từ phần còn lại (n-1) và các số đọc hiện tại của con quay hồi chuyển
Chúng ta sử dụng những giá trị nào để tính ước lượng được cập nhật Rest (n)? Bạn có thể đoán rằng chúng tôi sẽ sử dụng cả hai. Chúng tôi sẽ sử dụng giá trị trung bình có trọng số, để:
Phần còn lại (n) = (Racc * w1 + Rgyro * w2) / (w1 + w2)
Chúng ta có thể đơn giản hóa công thức này bằng cách chia cả tử số và mẫu số của phân số cho w1.
Phần còn lại (n) = (Racc * w1 / w1 + Rgyro * w2 / w1) / (w1 / w1 + w2 / w1)
và sau khi thay thế w2 / w1 = wGyro, chúng ta nhận được:
Phần còn lại (n) = (Racc + Rgyro * wGyro) / (1 + wGyro)
Trong diễn đàn ở trên, wGyro cho chúng ta biết mức độ tin tưởng của chúng ta đối với con quay hồi chuyển so với gia tốc kế của chúng ta. Giá trị này có thể được chọn bằng thực nghiệm thường các giá trị từ 5..20 sẽ kích hoạt kết quả tốt.
Sự khác biệt chính của thuật toán này so với bộ lọc Kalman là trọng số này tương đối cố định, trong khi trong bộ lọc Kalman, trọng số được cập nhật vĩnh viễn dựa trên tiếng ồn đo được của các số đọc gia tốc kế. Bộ lọc Kalman tập trung vào việc cung cấp cho bạn kết quả lý thuyết "tốt nhất", trong khi thuật toán này có thể cung cấp cho bạn kết quả "đủ tốt" cho ứng dụng thực tế của bạn. Bạn có thể triển khai một thuật toán điều chỉnh wGyro tùy thuộc vào một số yếu tố nhiễu mà bạn đo lường, nhưng các giá trị cố định sẽ hoạt động tốt đối với hầu hết các ứng dụng.
Chỉ còn một bước nữa là chúng ta có thể nhận được các giá trị ước tính được cập nhật của mình:
RxEst (n) = (RxAcc + RxGyro * wGyro) / (1 + wGyro) RyEst (n) = (RyAcc + RyGyro * wGyro) / (1 + wGyro) RzEst (n) = (RzAcc + RzGyro * wGyro) / (1 + wGyro)
Bây giờ, hãy chuẩn hóa lại vectơ này:
R = SQRT (RxEst (n) ^ 2 + RyEst (n) ^ 2 + RzEst (n) ^ 2)
RxEst (n) = RxEst (n) / R RyEst (n) = RyEst (n) / R RzEst (n) = RzEst (n) / R
Và chúng tôi đã sẵn sàng lặp lại vòng lặp của mình một lần nữa.
Hướng dẫn này ban đầu xuất hiện trên starlino.com, tôi đã thực hiện một vài chỉnh sửa nhẹ và đăng lại với sự cho phép. Cảm ơn Starlino!
Đề xuất:
Stone Lcd + Cảm biến con quay hồi chuyển gia tốc: 5 bước
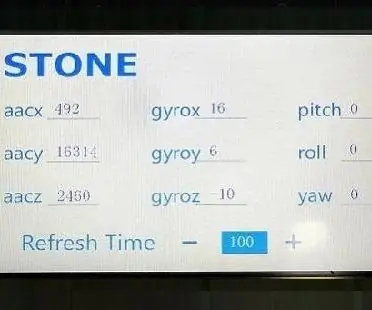
Cảm biến con quay hồi chuyển gia tốc Stone Lcd +: Tài liệu này sẽ dạy bạn cách sử dụng cảm biến con quay hồi chuyển gia tốc STM32 MCU + MPU6050 + màn hình cổng nối tiếp STONE STVC070WT cho DEMO.STVC070WT là màn hình nối tiếp của công ty chúng tôi, sự phát triển của nó rất đơn giản, dễ sử dụng , bạn có thể đến với chúng tôi
Bộ điều khiển Xbox 360 Gia tốc / Chỉ đạo con quay hồi chuyển Mod: 7 bước

Bộ điều khiển Xbox 360 Chế độ gia tốc / con quay hồi chuyển: Tôi đã chơi Assetto Corsa bằng bộ điều khiển Xbox 360 của mình. Thật không may, tay lái bằng cần điều khiển tương tự rất khó sử dụng và tôi không có không gian để thiết lập bánh xe. Tôi đã cố gắng nghĩ ra những cách có thể biến một cơ chế lái tốt hơn thành t
MPU6050-Gia tốc kế + Khái niệm cơ bản về cảm biến con quay hồi chuyển: 3 bước

Thông tin cơ bản về MPU6050-Accelerometer + Gyroscope Sensor: MPU6050 là một cảm biến rất hữu ích. Mpu 6050 là một IMU: Đơn vị đo lường quán tính (IMU) là một thiết bị điện tử đo lường và báo cáo lực cụ thể của cơ thể, tốc độ góc và đôi khi là hướng của cơ thể, sử dụng kết hợp
Con quay hồi chuyển gia tốc 3 trục GY-521 MPU6050 Hướng dẫn sử dụng mô-đun 6DOF: 4 bước

Con quay hồi chuyển gia tốc 3 trục GY-521 MPU6050 Hướng dẫn sử dụng mô-đun 6DOF: Mô tả Mô-đun đơn giản này chứa mọi thứ cần thiết để giao tiếp với Arduino và các bộ điều khiển khác thông qua I2C (sử dụng thư viện Wire Arduino) và cung cấp thông tin cảm biến chuyển động cho 3 trục - X, Y và Z .Đặc điểm kỹ thuật Phạm vi đo tốc độ: ± 2, ±
Arduino Nano và Visuino: Chuyển đổi gia tốc thành góc từ cảm biến gia tốc và con quay hồi chuyển MPU6050 I2C: 8 bước (có hình ảnh)
Arduino Nano và Visuino: Chuyển đổi gia tốc thành góc từ cảm biến gia tốc kế và con quay hồi chuyển MPU6050 I2C: Một thời gian trước, tôi đã đăng một hướng dẫn về cách bạn có thể kết nối Cảm biến gia tốc, con quay hồi chuyển và la bàn MPU9250 với Arduino Nano và lập trình nó với Visuino để gửi dữ liệu gói và hiển thị nó trên Phạm vi và Dụng cụ trực quan. Gia tốc kế gửi X, Y,
